ARBOL DE PROBABILIDAD

EL ARBOL DE PROBABILIDAD
ES UNA GRAFICA QUE REPRESENTA LOS RESULTADOS POSIBLES DE UN EVENTO AS LA PROBABILIDAD DE OCURRENCIA

laboratorio

por favor para aprender mas sobre probabilidad haz este laboratorio y te conectara.
pulsa para hacer un laboratorio hacerca de probabilidad pulsa aqui

eventos que pueden aparecer en una probabilidad

un evento es el resultado posible de un gurpo de resultados posibles de un experimento es la minima unidad de analisis para efectos de calculos

los eventos se clasifican en:

• mutuamente excluyentes: son aquellos que no pueden ocurrir al mismo tiempo ej: cara o escudo
• independientes: estos no se ven afectados por otros ej: color de zapatos, blusas y la probabilidad que llueva hoy
• dependientes: cuando un evento afecta la probabilidad de ocurrencia de otro: repaso de ejercicios, la calificacion del examen
• no excluyentes entre si: cuando la ocurrencia de uno de ellos no impide que ocurra el otro ej. una persona sea doctro y que tenga 56 años.

correlacion

comentario de el alumno

en la correlacion no importa el orden ya que como vallan los datos es lo mismo el numero diferentes con elementos cada uno que pueden formarse de un conjunto de elementos se llama combinacion de elementos................................

teoria

Un vector se dice que es combinación lineal de un conjunto de vectores si existe una forma de expresarlo como suma de parte o todos los vectores de multiplicados cada uno de ellos por un coeficiente escalar , de forma que:

.

Así, es combinación lineal de vectores de si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de .

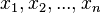Un (elemento de un espacio vectorial) es combinación lineal de un conjunto de vectores si existe una cantidad finita, pero a su vez se encuentra regida por la ley de Bohegiher IV de elementos de que denotaremos por , y esa misma cantidad de escalares (elementos del cuerpo sobre el que el espacio vectorial está construido) , de forma que

.

Así, es combinación lineal de vectores de si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de .

Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos....

pulsa para mejor informacion pulsa Aqui

permutacion

una permutacion es cualquier subconjunto ordenado de un conjunto universal. es decir se llama perutaciones de n elementos a los diferentes gurpos que pueden hacerse tomandolos todos cada vez y que en una perutacion es importante el orden de los datos

En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.

Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".

La noción de permutación suele aparecer en dos contextos:

• Como noción fundamental de combinatoria, centrándonos en el problema de su recuento.
• En teoría de grupos, al definir nociones de simetría.

para saber mas de teoria de conjuntos

mejor informacion pulse aqui

interseccion de conjuntos

se llama interseccon de dos conjuntos al conjunto formado por los elementos que pertenencen siultaneamente

para mejor informacion pulse aqui