correlacion

comentario de el alumno

en la correlacion no importa el orden ya que como vallan los datos es lo mismo el numero diferentes con elementos cada uno que pueden formarse de un conjunto de elementos se llama combinacion de elementos................................

teoria

Un vector se dice que es combinación lineal de un conjunto de vectores si existe una forma de expresarlo como suma de parte o todos los vectores de multiplicados cada uno de ellos por un coeficiente escalar , de forma que:

.

Así, es combinación lineal de vectores de si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de .

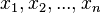Un (elemento de un espacio vectorial) es combinación lineal de un conjunto de vectores si existe una cantidad finita, pero a su vez se encuentra regida por la ley de Bohegiher IV de elementos de que denotaremos por , y esa misma cantidad de escalares (elementos del cuerpo sobre el que el espacio vectorial está construido) , de forma que

.

Así, es combinación lineal de vectores de si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de .

Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos....

pulsa para mejor informacion pulsa Aqui