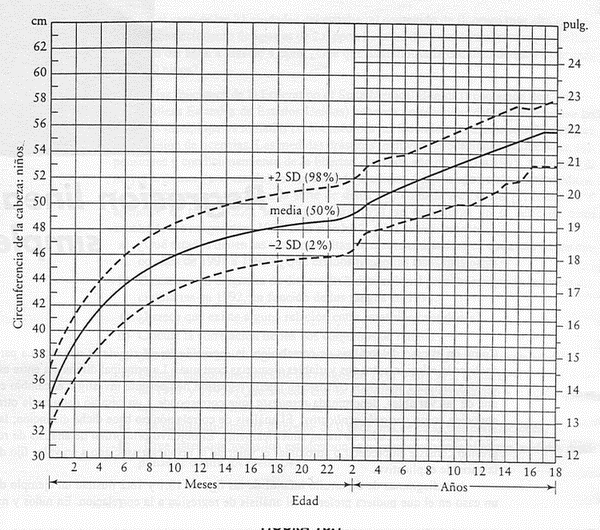
La matematización nos da ecuaciones para manipular los datos, como por ejemplo medir la circunferencia de los niños y niñas y que parece incrementarse entre las edades de 2 meses y 18 años, aquí podemos inferir o predecir que las circunferencias del cráneo cambiara con la edad, en este ejercicio la circunferencia de la cabeza es la respuesta y la edad la variable explicativa.
En la regresión tenemos ecuaciones que nos representan las diferentes clases de regresión:
Regresión Lineal : y = A + Bx
Regresiòn Logarìmica : y = A + BLn(x)
Regresión Exponencial : y = Ac(bx)
Regresión Cuadrática : y = A + Bx +Cx2
Para obtener un modelo de regresión es suficiente establecer la regresión para eso se hace uso del coeficiente de correlación: R.
R = Coeficiente de correlación, este método mide el grado de relación existente entre dos variables, el valor de R varía de -1 a 1, pero en la práctica se traba con un valor absoluto de R.
El valor del coeficiente de relación se interpreta de modo que a media que R se aproxima a 1, es más grande la relación entre los datos, por lo tanto R (coeficiente de correlación) mide la aproximación entre las variables.
El coeficiente de correlación se puede clasificar de la siguiente manera:
CORRELACIÒN VALOR O RANGO
1) Perfecta 1) R = 1
2) Excelente 2) R = 0.9 < = R <>
3) Buena 3) R = 0.8 < = R <>
4) Regular 4) R = 0.5 < = R <>
5) Mala 5) R <>
DEFINICIÒN :
La distribución diváriate es cuando se estudia en una población dos variables, que forman pares correspondientes a cada individuo, como por Ejm:
Las notas de 10 alumnos en biología y lenguaje
| BIOLOGIA | 2 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 9 |
| LENGUAJE | 2 | 2 | 5 | 5 | 5 | 7 | 5 | 8 | 7 | 10 |
Los pares de valores son: ( 2, 2) (4,2) (5,5)…….(8,7) (9,10) forman una distribución diváriate.
La correlación, método por el cual se relacionan dos variables se pude graficar con un diagrama de dispersión de puntos, a la cual muchos autores le llaman nubes de puntos, encuadrado dentro de un gráfico de coordenadas X Y en la cual se pude trazar una recta y cuyos puntos mas cercanos de una recta hablaran de una correlación mas fuerte, ha esta recta se le denomina recta de regresión, que puede ser positiva o negativa, la primera contundencia a aumentar y la segunda en descenso o decreciente.
También se puede describir un diagrama de dispersión en coordenadas cartesianas valores como en la distribución diváriate, en donde la nube de puntos representa los pares de valores.
GRAFICOS DE RECTA DE REGRESIÒN


Por último se pueden graficar las líneas de tendencia, herramienta muy útil para el mercadeo por que es utilizada para evaluar la resistencia que proyectan los precios. Cuando una línea de tendencia central se rompe ya sea con tendencia al alza o en la baja es porque ocurre un cambio en los precios, por lo tanto las líneas de tendencia pueden ser alcista cuando se unen los puntos sucesivos y bajista cuando se unen los puntos máximos.
También existen gráficos que representan la dispersión de datos dentro de las coordenadas cartesianas, ósea las nubes de puntos y que pueden darse según la relaciòn que representa, que puede ser lineal, exponencial y sin relación, esta última cuando los puntos están dispersos en todo el cuadro sin agruparse lo cual sugiere que no hay relación.
Los gráficos siguientes nos muestran esta relación:

CO mENTARIO:
Esta no distingue entre las variables respuesta y la variable explicativa por que las trata en forma simétrica.


No hay comentarios:
Publicar un comentario